Vikus JvRensburg's Webpage

Under construction!

"The only way to learn mathematics is to do mathematics. That tenet is the foundation of the do-it-yourself, Socratic, or Texas method, the method in which the teacher plays the role of an omniscient but largely uncommunicative referee between the learner and the facts." – Paul Halmos

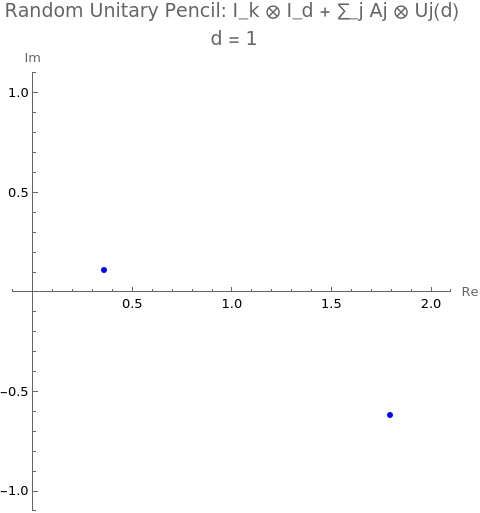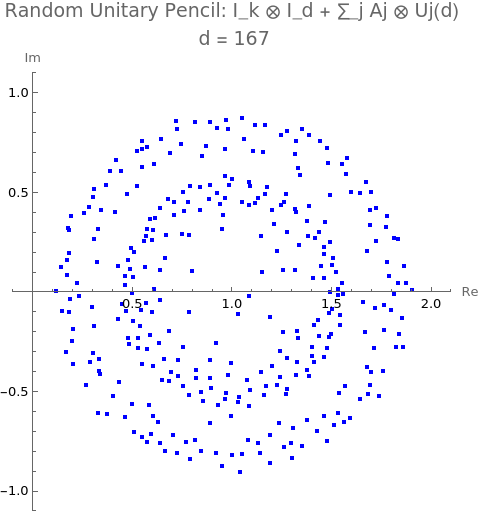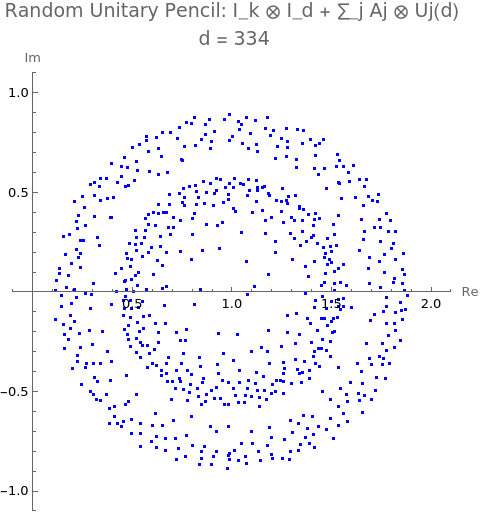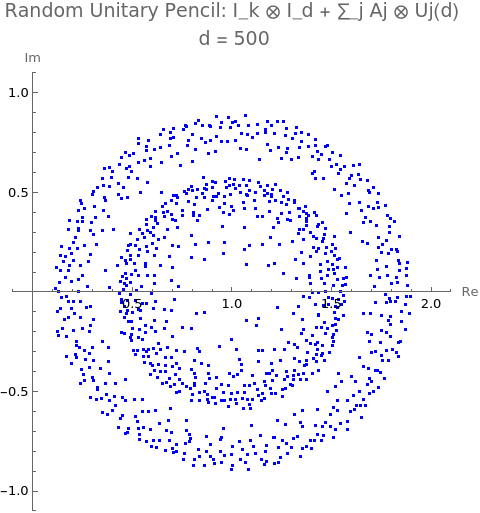
Eigenvalue development of a linear pencil evaluated at Haar unitaries — This animation shows the linear pencil \[ L_X(U_1,U_2) = I + X_1\otimes U_1 + X_2\otimes U_2 \] evaluated at two independent \( d \times d \) Haar-distributed random unitaries. The figure illustrates the development of the eigenvalues as the unitary dimension \( d \) increases.

\[ X_1 = \begin{pmatrix} 0.218011 & 0.218011 + 1.74409 i \\ 0 & 0 \end{pmatrix}, \qquad X_2 = \begin{pmatrix} 0 & 0.218011 + 1.74409 i \\ 0.218011 & 0.436022 \end{pmatrix}. \]